Question

The table shows how much a carpenter charges for work. Is the relationship shown by the data in the table linear? Explain your answer.

Answer 1

The relationship shown by the data in the table is not linear because the slope is not constant.

A linear function is a function that has a positive relationship between its variables.

Therefore, an increase in one variable (input variable) causes an increase in the other variable (output variable) because the variables are directly proportional.

Mathematically, the graph of a linear function is a straight-line and its slope is always constant.

Now , we would find the slope of the data:

`Slope = (40 - 25)/(2 - 1)\\\\Slope = (15)/(1)`

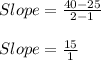
Slope = 15

`Slope = (60 - 40)/(3 - 2)\\\\Slope = (20)/(1)`

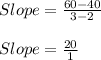
Slope = 20

Since the slope is not constant, the relationship shown by the data in the table is not linear.

Answer 2

It is not linear.

Explanation:

If it were, than for every change in hours worked, the slope of the line would be the same (or the cost would change be the same amount).

From 2 to 3 and 3 to 4 hours, the change in cost is $20. However, from 1 to 2 hours the change is $15.

Since it is not uniform, it is not linear.