Question

Solve the following problem:


Find x, y, u, v

Answer 1

X = 9, Y = 12, U = 24, V = 36

Explanation:

Answer 2

x = 9, y = 12, u = 24 and v = 32

Explanation:

In this case, we need to use the proportionality theorem, which states that a pair parallels intersected by two transversals creates proportional relations between resulting segments.

Also, this theorem is used to show similar triangles, like this case.

Notice that the base of each angle increased by a specific factor.

Using the theorem, we can create the following proportions.

Triangle 1 and Triangle 2.

`(3)/(3+x)=(5)/(20)\\(60)/(5)=3+x\\x=12-3=9`

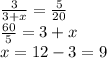
Also,

`(4)/(4+y) =(5)/(20)\\(80)/(5)=4+y\\ y+4=16\\y=16-4\\y=12`

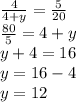
Triangle 2 and Triangle 3.

`(12)/(12+u) =(20)/(60)\\ (12)/(12+u) =(1)/(3)\\36=12+u\\u=36-12=24`

`(16)/(16+v) =(20)/(60)\\ (16)/(16+v) =(1)/(3)\\48=16+v\\v=48-16=32`

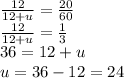
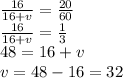
Therefore, the answers are x = 9, y = 12, u = 24 and v = 32.