Question

On Monday lance ran 30 min and swam 20 min. His fitness app told him he burned 610 calories. On Wednesday the fitness app told him he burned 695 calories when he ran 25 min and swam 40 min. How many calories he burned for one min?

Answer 1

15 calories while running.

8 calories while swimming.

Why?

To solve the problem, we need to create a system of equations (two equations and two variables)

Let be "x" the number of calories burned by running and "y" the number of calories burned by swimming.

So,

On Monday we have:

`30x+20y=610calories`

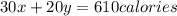
On Wednesday we have:

`25x+40y=695`

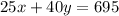
Now, we have the following system:

`\left \{ {{30x+20y=610} \atop {25x+40y=695}} \right.`

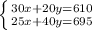
Solving, we have:

Multiplying the first equation by 2, and substracting the second equation from the first equation, we have:

`\left \{ {{30x*2+20y*2=610*2} \atop {25x+40y=695}} \right.\\\\\left \{ {{60x+40y=1220} \atop {25x+40y=695}} \right.\\\\(60x-25x)+(40y-40y)=1220-695\\\\35x=525\\\\x=15`

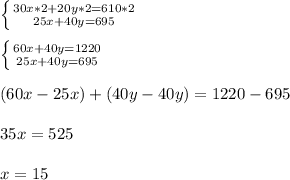
Now, substituting "x" into the first equation to calculate "y", we have:

`30*(15)+20y=610\\\\450+20y=610\\\\20y=610-450\\\\y=8`

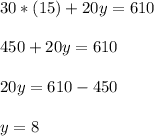
Hence, we have that He burned 15 calories per minute while running and 8 calories per minute while swimming.

Have a nice day!