Question

Lenny makes $55,000 and is getting annual raises of $2,500. Karl makes $62,000 with annual raises of $2,000. How many years, y, will it take for Lenny and Karl to make the same salary?

Answer 1

14 years

Explanation:

`y` represents number of years it will take for Lenny and Karl to earn same salary.

Lenny make $55,000 and annual raise is $2,500 per year.

So, in
`y` years Lenny would make in dollars =
`55,000+2,500y`

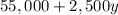
Karl makes $62,000 with annual raises of $2,000 per year.

So, in
`y` years Karl would make in dollars =
`62,000+2,000y`

We know that their salaries would be equal.

So, we have

`55000+2500y=62000+2000y`

subtracting both sides by
`2000y`

`55000+2500y-2000y=62000+2000y-2000y`

`55000+500y=62000`

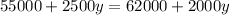
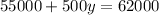
Subtracting both sides by 55000

`55000+500y-55000=62000-55000`

`500y=7000`

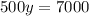
Dividing both sides by 500.

`(500y)/(500)=(7000)/(500)`

`y=14`

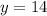
∴ In 14 years Lenny and Karl would make same salary.