Question

Lon Giron knows that his golf score is inversely related to the number of times he plays a week. When he plays 30 times a month, his average score is 85. What would his average score be if he played 35 times a month?

a. 32.8
b. 80.9
c. 80
d. 72.9

Answer 1

B i did this test it was right

Answer 2

Option D

Average score is 72.9 if he played 35 times a month

Solution:

Given that Lon Giron knows that his golf score is inversely related to the number of times he plays a week

`\text {golf score} \space \alpha \frac{1}{\text { number of times he plays a week }}`

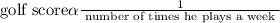
Given that When he plays 30 times a month, his average score is 85

Number of times he plays in a month = 30

average score = 85

`85 \alpha (1)/(30)`

`85=k (1)/(30)`

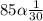
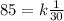
Where "k" represents constant of propotionality

`k=30 * 85=2550`

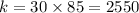
Thus we have found out value of k as 2550

Now if he played 35 times a month, we have to find his average score

Let the required average score be "a"

Let us use the value of "k"

`\begin{array}{l}{a=k (1)/(35)} \\\\ {a=2550 * (1)/(35)=72.85}\end{array}`

a = 72.85 ≈ 72.9

Thus average score is 72.9 if he played 35 times a month