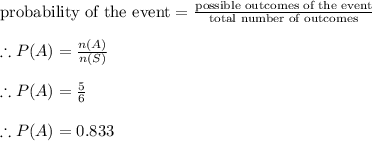Question

Find the probability of rolling a number less than 6 on 1 roll of a die

Answer 1

The probability of rolling a number less than 6 on 1 roll of a die is

`(5)/(6)` = 0.833is

Explanation:

Let

S be the sample space for a rolling of a Die

∴ is total number of outcomes for a rolling of a die are ={ one, two, three, four, five, six} six

i.e { 1,2,3,4,5,6}

∴ n (S) = 6

let A be the event of getting a number less than six

then the possible outcomes are { 1, 2, 3, 4, 5 }

∴ n(A) = 5

To Find:

P (A) = ?

Solution:

we know that probability is given by

`\textrm{probability of the event}=\frac{\textrm{possible outcomes of the event}}{\textrm{total number of outcomes}} \\\\\therefore P(A) = (n(A))/(n(S)) \\\\\therefore P(A) =(5)/(6)\\ \\\therefore P(A) = 0.833\\`