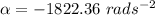Question

An optical disk drive in a computer can spin a disk at up to 10,000 rpm. If a particular disk is spun at 7570 rpm while it is being read, and then is allowed to come to rest over 0.435 s, what is the magnitude of the average angular acceleration of the disk?

Answer 1

`1822.36\ rad/s^2`

Step-by-step explanation:

given,

speed of the disk = 7570 rpm

time of rest of the disk = 0.435 s

average angular acceleration = ?

initial speed of disk = 7570 rpm

=
`7570 * (2\pi)/(60)`

=
`792.73\ rad/s`

final angular velocity = 0 rad/s

average angular acceleration =
`(\omega_f-\omega_i)/(t)`

=
`(0 -792.73)/(0.435)`

=
`1822.36\ rad/s^2`

the average angular acceleration =
`1822.36\ rad/s^2`

Answer 2

The magnitude of the average angular acceleration is calculated as
`1822.36\ rad/s^(2)`

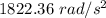
Step-by-step explanation:

Maximum speed that can be attained by the disk,
`N_(m)` = 10,000 rpm

Speed of spinning of the disk, N = 7570 rpm

Time taken to come to rest, t = 0.435 s

Now,

The initial angular velocity is given by:

`\omega = (2\pi N)/(60) = 792.73\ rads^(-1)`

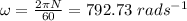
Final angular velocity,
`\omega' = 0\ rads^(- 1)`

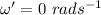
The average angular acceleration of the disk can be computed by using the kinematic eqn:

`\omega' = \omega + \alpha t`

`0 = 792.73 + 0.435\alpha`

`\alpha = - 1822.36\ rads^(- 2)`