Question

In​ 2012, the population of a city was 6.27 million. The exponential growth rate was 1.47​% per year.

​a) Find the exponential growth function.
​b) Estimate the population of the city in 2018.
​c) When will the population of the city be 8 ​million?
​d) Find the doubling time.

Answer 1

a)
`a(t)= 6.27e^(0.0147*t)`

b) 6.84 million

c) 2028.52

d) 47 years

Explanation:

a)Here we know standard exponential growth rate is

`a(t)= ae^(k*t)`

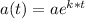
In this put t=0 and a(t)=6.27 million

thus we get a = 6.27 million

now
`(da)/(dt)=a(t)k`

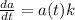
this is equal to(in 2012)=
`(1.47)/(100)*=0.0147`

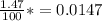
b)Put t = 6

we get

`a(t)= 6.27e^(0.0147*6)`

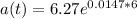
=6.84 million

c)
`8 = 6.27e^(0.0147*t)`

take log both sides

we get 16.52 years

d)
`2*6.27=6.27e^(0.0147*t)`

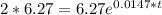
take log both sides we get 47 years to get double the current population.