Question

A Food Marketing Institute found that 39% of households spend more than $125 a week on groceries. Assume the population proportion is 0.39 and a simple random sample of 87 households is selected from the population. What is the probability that the sample proportion of households spending more than $125 a week is between 0.29 and 0.41?

Answer 1

0.6210

Explanation:

Given that a Food Marketing Institute found that 39% of households spend more than $125 a week on groceries

Sample size n =87

Sample proportion will follow a normal distribution with p =0.39

and standard error =
`\sqrt{(0.39(1-0.39))/(87) } \\=0.0523`

the probability that the sample proportion of households spending more than $125 a week is between 0.29 and 0.41

=
`P(0.29<p<0.41)\\\\ =0.64892-0.02794\\=0.6210`

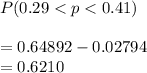
There is 0.6210 probability that the sample proportion of households spending more than $125 a week is between 0.29 and 0.41