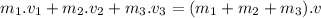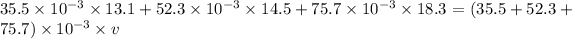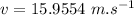Answer:
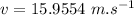
Step-by-step explanation:
Given:
- mass of the honey drop 1,
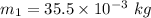
- velocity of the honey drop 1,
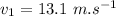
- mass of the honey drop 2,
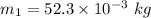
- velocity of the honey drop 2,
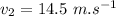
- mass of the honey drop 3,
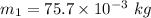
- velocity of the honey drop 3,

In ISS there is zero gravity an the collision is completely inelastic.
So, applying the law of conservation of momentum: