Question

A college student completed some courses worth 3 credits and some courses worth 4 credits. The student earned a total of 59 credits after completing 18 courses.

How many courses worth 2 credits did the student complete?

Answer 1

He completed 13 courses worth 3 credits and 5 courses worth 4 credits.

Explanation:

Let

Number of courses worth 3 credits = x

Number of courses worth 4 credits = y

1. The student completed a total of 18 courses, then

`x+y=18`

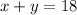
2. The student earned a total of 59 credits, he earned 3x on 3 credits' courses and 4y on 4 credits' courses, so

`3x+4y=59`

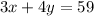
3. You get the system of two equations:

`\left\{\begin{array}{l}x+y=18\\ \\3x+4y=59\end{array}\right.`

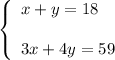
From the first equation

`x=18-y`

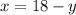
Substitute it into the second equation:

`3(18-y)+4y=59\\ \\54-3y+4y=59\\ \\4y-3y=59-54\\ \\y=5\\ \\x=18-5=13`

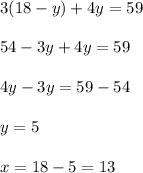
He completed 13 courses worth 3 credits and 5 courses worth 4 credits.