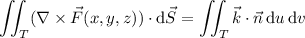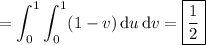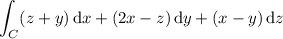
has the underlying vector field
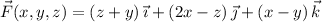
with curl
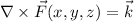
Parameterize
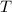 by
by
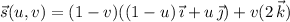
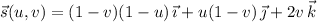
with
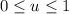 ,
,
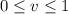 .
.
The implied orientation of the curve is counter-clockwise when viewing
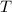 from the first octant (each of
from the first octant (each of
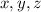 greater than 0), so that the normal vector to
greater than 0), so that the normal vector to
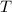 is pointing upward and away from the origin. Take this vector to be
is pointing upward and away from the origin. Take this vector to be
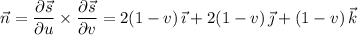
Then by Stokes' theorem, the line integral is equivalent to