Question

The owner of a computer repair shop has determined that their daily revenue has mean $7200 and standard deviation$1200. The daily revenue totals for the next 30 days will be monitored. What is the probability that the mean daily revenuefor the next 30 days will exceed $7500

Answer 1

The probability that the mean daily revenue for the next 30 days will exceed $7500 is 0.0855

Explanation:

It has been given that

`\mu=7200\\\\\sigma=1200,n=30,x=7500`

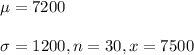
Now, the formula for z-score of a normal distribution is given by

`z=(x-\mu)/((\sigma)/(√(n)))`

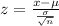
Substituting the known values, we get

`z=(7500-7200)/((1200)/(√(30)))`

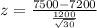
Simplifying, we get

`z=(300)/(219.1)\\\\z=1.369238`

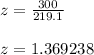
Now, we have to find that the daily revenue for next 30 days will exceed $7500.

Thus, we have to find

P(z>1.369238)

From the normal distribution table, we have

P(z>1.369238)= 0.0855

Therefore, required probability is 0.0855