Question

Water, which we can treat as ideal and incompressible, flows at 12 m/s in a horizontal pipe with a pressure of 3.0 × 10^4 Pa.

If the pipe widens to twice its original radius, what is the pressure in the wider section?

Answer 1

9.8 × 10⁴Pa

Step-by-step explanation:

Given:

Velocity V₁ = 12m/s

Pressure P₁ = 3 × 10⁴ Pa

From continuity equation we have

ρA₁V₁ = ρA₂V₂

A₁V₁ = A₂V₂

making V₂ the subject of the equation;

`V_(2) = (A_(1)V_(1))/(A_(2))`

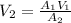
the pipe is widened to twice its original radius,

r₂ = 2r₁

then the cross-sectional area A₂ = 4A₁

⇒
`V_(2)= (A_(1)V_(1))/(4A_(1))`

`V_(2)= (V_(1))/(4)`

This implies that the water speed will drop by a factor of
`(1)/(4)` because of the increase the pipe cross-sectional area.

The Bernoulli Equation;

Energy per unit volume before = Energy per unit volume after

p₁ +
`(1)/(2)`ρV₁² + ρgh₁ = p₂ +
`(1)/(2)`ρV₂² + ρgh₂

Total pressure is constant and
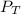`P_(T)` = P =
`(1)/(2)`ρV₂²ρV²

p₁ +
`(1)/(2)`ρV₁² = p₂ +
`(1)/(2)`ρV₂²

Making p₂ the subject of the equation above;

p₂ = p₁ +
`(1)/(2)`ρV₁² -
`(1)/(2)`ρV₂²

But
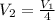`V_(2)  = (V_(1))/(4)` so,

p₂ = p₁ +
`(1)/(2)`ρV₁² -
`(1)/(2)`ρ
`(V_(1)^(2))/(4^(2))`

p₂ = 3.0 x 10⁴ + (
`(1)/(2)` × 1000 × 12²) - (
`(1)/(2)` × 1000 × 12²/4² )

P₂ = 3.0 x 10⁴ + 7.2 × 10⁴ - 4.05 x 10³

P₂ = 9.79 × 10⁴Pa

P₂ = 9.8 × 10⁴Pa