Question

The nose of an ultra-light plane is pointed is pointed South and its airspeed indicator shows 35m/s. The plane is in a 10m/s wind blowing towards the SouthWest relative to the ground. What is the plane's speed with respect to ground?

Answer 1

The plane's velocity is
`(v_(x),v_(y))=(-7.07,-42.07)`.

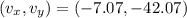Step-by-step explanation:

Given that,

Airspeed v= 35 m/s

Speed of wind v'= 10 m/s

Let x be the east and y be the north.

We need to calculate the velocity along the x -direction

Using velocity component

`v_(x)=-v'\cos\theta`

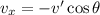
Put the value into the formula

`v_(x)=-10\cos45`

`v_(x)=-7.07\ m/s`

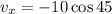
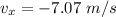
We need to calculate the velocity along the y -direction

Using velocity component

`v_(y)=-(v'\sin\theta+v)`

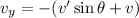
Put the value into the formula

`v_(y)=-(10\sin45+35)`

`v_(y)= -42.07\ m/s`

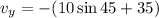
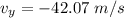
Hence, The plane's velocity is
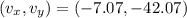`(v_(x),v_(y))=(-7.07,-42.07)`.

Answer 2

`v=42.66\ m.s^(-1)`

`\beta=6.75^(\circ)` clockwise from the south.

Step-by-step explanation:

Given:

• velocity of the plane southwards,
  `v_p=35\ m.s^(-1)`

• velocity of the wind in south-west,
  `v_w=10\ m.s^(-1)`

• ∴Angle between the plane and wind velocities,
  `\theta=45^(\circ)`

According to the vector addition rule, magnitude of the resultant velocity is given as:

`v=√(v_p^2+v_w^2+2* v_p.v_w\ cos\ \theta)`

`v=√(35^2+10^2+2* 35* 10\ cos\ \45)`

`v=42.66\ m.s^(-1)` is the plane's speed with respect to ground.

Direction of this resultant with respect to south:

`tan\ \beta=(v_w\ sin\theta)/((v_p+v_p\ cos\theta))`

`tan\ \beta=(10\ sin\ 45)/((35+35\ cos\ 45))`

`\beta=6.75^(\circ)` clockwise from the south.