Question

Let ABC be a triangle with centroid G. Points L, M, and N are the midpoints of sides BC, CA, and AB respectively. Let D be the foot of the altitude from A to BC and let K be the foot of the altitude from L to MN.

(a) Show that AD/LK=2

(b) Show that triangleADG is similar to triangleLKG

(c) Show that D, G and K are collinear and that DG/GK=2

Answer 1

See explanation

Explanation:

1. MN is the midline of the triangle ABC. By the midline theorem, MN is parallel to BC. AD is perpendicular to BC, KL is perpendicular to MN, so KL is perpendicular to BC. Two perpendicular lines to BC are parallel, thus

AD ║ KL.

In quadrilateral EDLK,

ED ║ KL

DL ║ EK,

so EDLK is a parallelogram.

Opposite sides of the parallelogram are congruent, so

`KL\cong ED`

Midline MN of the triangle ABC divides the height AD into two congruent parts AE and ED. So,

`KL=ED=(1)/(2)AD\Rightarrow (AD)/(LK)=2`

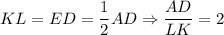
2. Since AD ║ KL, then

∠DAG ≅ ∠GLK

as alternate interior angles when parallel lines AD and KL are cut by transversal AL.

Since G is centroid, then

`(AG)/(GL)=(2)/(1)`

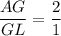
By SAS similarity theorem,
`\triangle ADG \sim \triangle LKG`

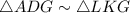
3. If
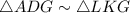`\triangle ADG \sim \triangle LKG` then

∠DGA ≅ ∠KGL

Since points A, G and L lie on the same line AL, then points D, G and K lie on the same line DK, so they are collinear