Answer:
Approximately 6.81 × 10⁵ Pa.
Assumption: carbon dioxide behaves like an ideal gas.
Step-by-step explanation:
Look up the relative atomic mass of carbon and oxygen on a modern periodic table:
Calculate the molar mass of carbon dioxide
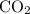 :
:
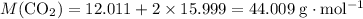 .
.
Find the number of moles of molecules in that
 sample of
sample of
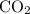 :
:
 .
.
If carbon dioxide behaves like an ideal gas, it should satisfy the ideal gas equation when it is inside a container:
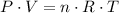 ,
,
where
 is the pressure inside the container.
is the pressure inside the container.
 is the volume of the container.
is the volume of the container.
 is the number of moles of particles (molecules, or atoms in case of noble gases) in the gas.
is the number of moles of particles (molecules, or atoms in case of noble gases) in the gas.
 is the ideal gas constant.
is the ideal gas constant.
 is the absolute temperature of the gas.
is the absolute temperature of the gas.
Rearrange the equation to find an expression for
 , the pressure inside the container.
, the pressure inside the container.
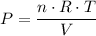 .
.
Look up the ideal gas constant in the appropriate units.
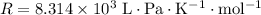 .
.
Evaluate the expression for
 :
:
 .
.
Apply dimensional analysis to verify the unit of pressure.