Question

An object launched straight up at a speed of 29.4 meters per second has a height, h, in meters of h , t seconds after the object is launched. What is the maximum height that the object will reach? Why does t have to be between zero and six? (This problem d

Answer 1

h = 44.06 meters (maximum height)

the time the object takes to complete this whole path is 6 seconds, this is why the time at which the object reaches its maximum height will between 0 and 6 seconds

Explanation:

To solve this question, we need to first recognize that this is a constant acceleration problem, specifically, it can be thought of as a projectile motion problem.

Recall, the equations of motion:

`1) v^2 - v_0^2 = 2a(s - s_0)\\2) s = v_0^2  + (1)/(2) at^2\\3) v = v_0 + at`

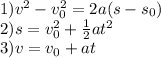
What do we already know?

• 
  `v_0 = 29.4 ms^-1`
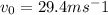
• The launch is straight up
• 
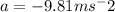  `a = -9.81 ms^-2` this is the gravitational acceleration
  `g`

• 
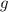
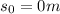  `s_0 = 0 m`, since our reference point is at s = 0, (the ground)

We can use use the Eq(1):

we know that when any object is launched up, at maximum height its velocity is going to be zero,
`v = 0 ms^-2`

`v^2 - v_0^2 = 2a(s - s_0)\\0^2 - (29.4)^2 = 2(-9.81)(s- 0)\\s = 44.06 m`

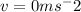
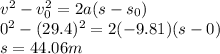
this is the maximum height!

Why does t have to between zero and six?

We can answer this using a bit visualization, if you think about the second equation

`s = v_0 t - (1)/(2)at^2\\ s = 29.4t - 4.905t^2`

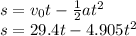
this is the equation of the whole trajectory that object makes.

and if you solve this by making
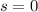`s = 0`, you will get the times at which the object was at the ground. the times will be 0s and 5.99s.

so the amount of time the object takes to go through this whole path is 6 seconds and this why the object will only reach its maximum height in between this time interval.

hope this helps :)