Question

A rectangular piece of​ cardboard, whose area is 374 square​ centimeters, is made into an open box by cutting a 2​-centimeter square from each corner and turning up the sides. If the box is to have a volume of 468 cubic​ centimeters, what size cardboard should you start​ with?

Answer 1

Answer with Step-by-step explanation:

Let length of rectangular piece of cardboard=x

Width of rectangular piece of cardboard=y

Area of rectangular piece of cardboard=
`374 cm^2`

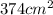
Area of rectangular piece of cardboard
`=l* b=x* y`

`xy=374`

`y=(374)/(x)`

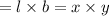
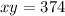
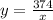
According to question

Length of box=x-2(2)=x-4

Width of box=y-2(2)=y-4

Height of box=2

Volume of box=
`l* b* h`

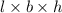
Substitute the values in this formula

Volume of box=
`2(x-4)(y-4)`

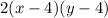
Substitute the value of y

`2(x-4)((374)/(x)-4)=468`

`((x-4)(374-4x))/(x)=(468)/(2)=234`

`(x-4)(374-4x)=234x`

`374x-4x^2-1496+16x=234x`

`4x^2-374x-16x+234x+1496=0`

`4x^2-156x+1496=0`

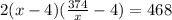
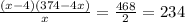
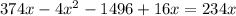
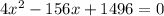
On dividing by 4 on both sides , then we get

`x^2-39x+374=0`

`x^2-17x-22x+374=0`

`x(x-17)-22(x-17)=0`

`(x-17)(x-22)=0`

`x-17=0`

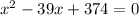
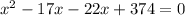
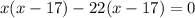
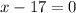
`x=17` or
`x-22=0\implies x=22`

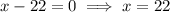
Substitute x=17

Then, we get
`y=(374)/(17)=22`

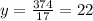
Substitute x=22

Then, we get

`y=(374)/(22)=17`

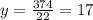
The size of cardboard should start with 17 by 22.