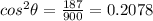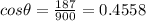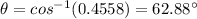Question

experiments show that the ground spider drassodes cupreus uses one of its several pairs of eyes as a polarization defector. In fact, the two eyes in this pair have polarization directions that are at right angles to one another. Suppose linearly polarized light with an intensity of 900W/m2 shines from the sky onto the spider, and that theintensity transmitted by one of the polarizing eyes is 187 W/m2.(a) For this eye, what is the angle between thepolarization direction of the eye and the polarization direction ofthe incident light?_____________?°

Answer 1

The angle is
`62.88^(\circ)`

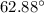
Solution:

As per the question:

Intensity of the linearly polarized light, I =
`900\ W/m^(2)`

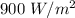
Intensity transmitted, I' =
`187\ W/m^(2)`

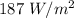
Now,

To calculate the angle between the polarization direction of the eye and that of the incident light:

`I' = Icos^(2)\theta`

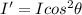
Thus Rearranging the eqn for the angle and using the suitable values in the above eqn:

`cos^(2)\theta = (187)/(900) = 0.2078`

`cos\theta = (187)/(900) = 0.4558`

`\theta = cos^(- 1)(0.4558) = 62.88^(\circ)`