Question

Find the radius R of the orbit of a geosynchronous satellite that circles the Earth. (Note that R is measured from the center of the Earth, not the surface of the Earth.) Use the following values if needed in this problem:

1) The universal gravitational constant G is 6.67×10−11Nm2/kg2.
2) The mass of the earth is 5.98×1024kg.
3) The radius of the earth is 6.38×106m.

Answer 1

R = 1.932 x 10⁸ m

Step-by-step explanation:

given,

gravitational constant = G = 6.67×10⁻¹¹ N.m²/kg²

mass of the earth = 5.98 x 10²⁴ Kg

radius of earth = 6.38 x 10⁶ m

equating gravitational force on the satellite with the centripetal force acting on it.

`(GMm)/(R^2) = (mv^2)/(R)`

`(GM)/(R^2) = (v^2)/(R)`

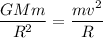
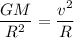
where v = R ω

`(GM)/(R^2) = (R^2\omega^2)/(R)`

`(GM)/(\omega^2) =R^3`

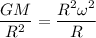
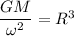
and
`\omega = (2\pi)/(T)`

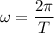
T = 84600 sec

`\omega = (2\pi)/(84600)`

`\omega =7.43 * 10^(-6)\ rad/s`

`R^3 = (6.67 * 10^(-11)* 5.98 * 10^(24))/((7.43 * 10^(-6))^2)`

`R^3 =7.22 * 10^(24)`

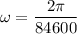
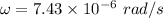
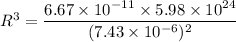
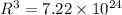
R = 1.932 x 10⁸ m