Question

It takes 3 hours to paddle a kayak 12 miles downstream and 4 hours for the return trip upstream. Find the rate of the kayak in still water

Answer 1

The rate of the kayak in still water is 3.5 mph

Solution:

Given that It takes 3 hours to paddle a kayak 12 miles downstream

Distance covered in downstream = 12 miles

Time taken to cover downstream = 3 hours

Also given that it takes 4 hours for the return trip upstream

Distance covered in upstream = 12 miles

Time taken to cover upstream = 4 hours

Formula to remember:

If the speed of a boat in still water is u km/hr and the speed of the stream is v km/hr, then: Speed downstream = (u + v) km/hr and Speed upstream = (u - v) km/hr

Let the speed of Kayak in still water = x mph

And The speed of current = y mph

For downstream:

Speed downstream = x + y

We know that
`speed = (distance)/(time)`

`(distance)/(time) = x + y`

`x + y = (12)/(3)`

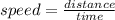
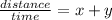
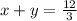
x + y = 4 ------ eqn 1

For upstream:

Speed upstream = x - y

`(12)/(4) = x - y`

x - y = 3 -------- eqn 2

Now let us eqn 1 and eqn 2

Add eqn 1 and eqn 2

x + y + x - y = 4 + 3

2x = 7

x = 3.5

speed of Kayak in still water = x mph = 3.5 mph