Question

The length of a rectangle is increasing at a rate of 8 centimeters per second and its width is increasing at a rate of 3 centimeters per second. When the length is 20 cm and the width is 10 cm, how fast is the area of the rectangle increasing?

Answer 1

Area of rectangle is increasing at 140 cm²/s when the length is 20 cm and the width is 10 cm.

Explanation:

Area = Length x Width

A = LW

Differentiating with respect to time

`(dA)/(dt)=L(dW)/(dt)+W(dL)/(dt)`

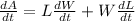
Length, L = 20 cm

Width, W = 10 cm

`(dW)/(dt)=3cm/s\\\\(dL)/(dt)=8cm/s`

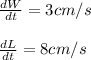
Substituting

`(dA)/(dt)=20* 3+10* 8\\\\(dA)/(dt)=60+80\\\\(dA)/(dt)=140cm^2/s`

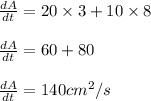
Area of rectangle is increasing at 140 cm²/s when the length is 20 cm and the width is 10 cm.