The time spent by bicyclist on entire trip is
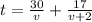
a) when v = 15 then t = 3 hours
b) when v = 18 then t = 2.52 hours
Solution:
The time taken is given by formula:
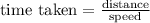
For the first 30 km, the bicyclist rode with a speed of v km/hour
Here distance = 30 km and speed = v km\hour
Let
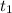 denote time taken to cover first 30 km
denote time taken to cover first 30 km
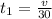
For the remaining 17 km he rode with a speed which was 2 km/hour greater than his original speed
so the speed to cover next 17 km = v + 2
Let
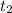 denote time taken to cover remaining 17 km
denote time taken to cover remaining 17 km
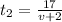
Now total time t spent by the bicyclist to cover entire trip is given by
total time "t" = time taken for first 30 km + time taken for remaining 17 km
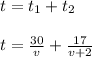
We have to find value of "t" for a) v = 15 and b) v = 18
a) value of t when v = 15
Substitute v = 15 in eqn 1
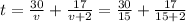
t = 2 + 1 = 3
So t = 3 hours
b) value of t when v = 18
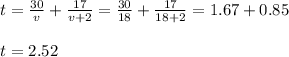
Thus t = 2.52 hours