Question

Two numbers add up to 23. 7 times the difference of the two numbers is 21. What are the two numbers?

Define the variables: let x = first number, let y = second number

Equation 1:

Equation 2:

Solve the system:

1st number:

2nd number:

Please show work on how to get the answers. Thanks!

Answer 1

Equation 1:
`x+y =23.`

Equation 2 :
`x-y =3.`

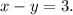
1st number: 13

2nd number: 10

Explanation:

Let the first number be x;

x = first number

Let the second number be y;

y = second number

Now Given, Two numbers add up to 23.

Hence the equation can be made as;

`x+y =23.`

Equation 1:
`x+y =23.`

Also Given, 7 times the difference of the two numbers is 21.

Hence the equation can be made as;

`7(x-y) =21`

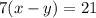
Dividing 7 on both side we get;

`(7(x-y))/(7) =(21)/(7)\\\\x-y = 3`

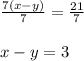
Equation 2 :
`x-y =3.`

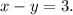
Now we will solve the system of equations we get;

We will add equation 1 and equation 2 we get;

`(x+y)+(x-y) =23+3\\x+y+x-y=26\\2x=26\\x = (26)/(2)=13`

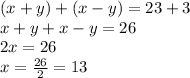
1st number: 13

Now Substituting the value of x in equation 1 we get;

`x+y=23\\13+y=23\\y=23-13\\y=10`

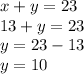
2nd number: 10

Hence Final Answer is.

Equation 1:
`x+y =23.`

Equation 2 :
`x-y =3.`

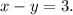
1st number: 13

2nd number: 10