Question

Richard has a 9-inch by 13.5-inch sheet of cardboard. He cuts squares from 4 corners to create an open container with the largest possible volume.

What is the greatest volume possible? Express your answer as a decimal to the nearest cubic inch.

Answer 1

96.256 in³

Explanation:

Given,

The dimension of the sheet = 9-inch by 13.5-inch,

Suppose x be the side of the square which is cut from each corner,

So, the dimension of the resultant open container,

(9-2x) inch × (13.5 - 2x) inch × x inch

Thus, the volume of the box,

V(x) = (9-2x) × (13.5 - 2x) × x

`V(x) = (9x-2x^2)(13.5 - 2x)`

Differentiating with respect to x,

`V'(x) = (9x - 2x^2)(-2) + (9 - 4x)(13.5 - 2x)`

`=-18x + 4x^2 + 121.5 - 18x - 54x + 8x^2`

`=12x^2 - 90x + 121.5`

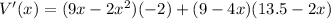
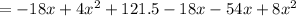
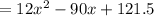
Again differentiating,

`V''(x) = 24x - 90`

For maxima or minima,

`V'(X) = 0`

`12x^2 - 90x + 121.5=0`

Using the quadratic formula,

`x =(90\pm √(90^2 - 4* 12* 121.5))/(24)`

`\implies x\approx 1.766\text{ or }x=5.734`

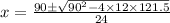
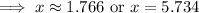
For x = 1.766, V''(x) = negative,

Thus, V(x) is maximum at x = 1.766,

For x =5.734, V''(x) = positive,

Thus, V(x) is minimum at x = 5.734,

Hence, the maximum possible volume, V(1.766) = (9-2(1.766)) × (13.5 - 2(1.766)) × 1.766

≈ 96.256 in³