Question

Engine 1 has an efficiency of 0.13 and requires 7200 J of input heat to perform a certain amount of work. Engine 2 has an efficiency of 0.28 and performs the same amount of work. How much input heat does the second engine require?

Answer 1

3,342.86J

Step-by-step explanation:

Engine 1

Quantity of Input Heat,
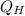`Q_(H)` = 7200J

Efficiency, η = 0.13

Efficiency, η
`=(W)/(Q_(H))`

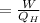
⇒ W = η
`Q_(H)`

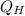
W = 0.13 × 7200

W = 936J

Engine 2

Efficiency, η = 0.28

Since Engine 2 performs same amount of work as Engine 1, then,

Work-done by Engine 2 = Work-done by Engine 1

W₂ = W₁ = 936J

Efficiency, η
`=(W)/(Q_(H))`

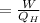
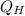`Q_(H)` = W / η

`Q_(H)=(936)/(0.28)`

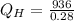
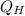`Q_(H)` = 3,342.86J

The input heat require by the second engine is 3,342.86J