The half-life of cobalt-60 is 5.26 years. After 10.52 years, 5 grams of a 20-gram sample will remain is TRUE
Step-by-step explanation:
Mass of cobalt = 20 g
Half-life = 5.26 years
Mass remains after 10.52 years = 5 g
This can be solved by using given below formula,

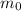 = initial mass
= initial mass
t = number of years from when the mass was m_0
m(t) = remaining mass after t years
Number of half-lives =
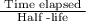
Number of half-lives =
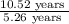
Number of half-lives = 2
At time zero = 20 g
At first half-life =
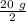 = 10 g
= 10 g
At second half life =
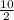 = 5 g
= 5 g
The given statement is true.