Question

For a circle with a diameter

of 6 meters, what is the measurement of a central angle (in degrees) subtended by an arc with a length of 5/2 pi meters

Answer 1

The measurement of the angle subtended by an arc with a length of 5/2 pi meters is 149.542°

Explanation:

Here, the diameter of the circle = 6 m

Diameter = 2 x RADIUS

So, radius = D / 2 = 6 / 2 = 3 m

Also, the length of the arc = (
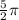`(5)/(2)  \pi`) meters

Putting π = 3.14, we get

The length S of the arc =
`(5)/(2)  * (3.14)  =  7.85`

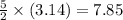
or, S = 7.85 m

Let us assume the arc subtends angle Ф at the center of the circle.

⇒ S = r Ф

or, Ф =
`(S)/(r)   = (7.85)/(3)  =  2.61`

⇒Ф = 2.61 radians

Now, 1 Radian = 57.2958 Degrees

⇒ 2. 62 Radian = 2.61 x ( 57.2958 Degrees) = 149.542 °

or, Ф = 149.542°

Hence, the measurement of the angle subtended by an arc with a length of 5/2 pi meters is 149.542°