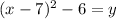Answer:
Explanation:
If you plot this point and the directrix on a coordinate plane, you can see that the directrix is 1/4 of a unit below the vertex. Since, by nature, a parabola opens in the direction opposite the directrix and "hugs" the focus, this is a positive x-squared parabola (meaning it opens upwards). The formula for this type of a parabola is, in vertex form,

where p is distance (in units) between the vertex and the directrix and h and k are the coordinates of the vertex. For us, p = .25, h = 7, and k = -6. Filling in our formula:
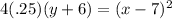
Simplify the left side to
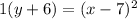 which simplifies, in its entirety, to
which simplifies, in its entirety, to