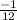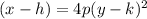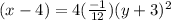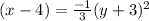Answer:
The equation of parabola is given by :
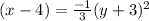
Explanation:
Given that vertex and focus of parabola are
Vertex: (4,-3)
Focus:(
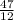 ,-3)
,-3)
The general equation of parabola is given by.
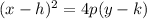 , When x-componet of focus and Vertex is same
, When x-componet of focus and Vertex is same
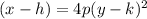 , When y-componet of focus and Vertex is same
, When y-componet of focus and Vertex is same
where Vertex: (h,k)
and p is distance between vertex and focus
The distance between two points is given by :
L=
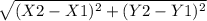
For value of p:
p=
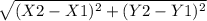
p=

p=
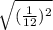
p=
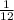 and p=
and p=
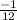
Since, Focus is left side of the vertex,
p=
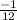 is required value
is required value
Replacing value in general equation of parabola,
Vertex: (h,k)=(4,-3)
p=