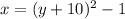Question

Using the given information, give the vertex form equation of each parabola.

Vertex:(-1,-10) Focus:(-3/4, -10)

Answer 1

Explanation:

If you plot these points on a coordinate plane, you will see that they both lie on the same horiztonal line, y = -10, with the focus 1/4 to the right of the vertex. This information tells you a ton of stuff. First, it tells you that, since a parabola "hugs" the focus, this parabola opens to the right and is of the form x = y-squared. This equation is

`4p(x-h)=(y-k)^2`

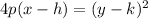
The information also tells us that p (the distance between the vertex and the focus) is .25. h is the "x" coordinate of the vertex and k is the "y" coordinate of the vertex, so h = -1, and k = -10. Filling in our formula:

`4(.25)(x+1)=(y+10)^2`

Simplify the left to

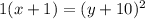`1(x+1)=(y+10)^2` and solve for x:

`x=(y+10)^2-1`