Question

A commuter train blows its 200-Hz horn as it approaches a crossing. The speed of sound is 335 m/s. (a) An observer waiting at the crossing receives a frequency of 208 Hz. What is the speed of the train? (b) What frequency does the observer receive as the train moves away?

Answer 1

The speed of the train, using the Doppler Effect, is found to be approximately 14.9 m/s as it approaches the observer, and the frequency heard as the train moves away is approximately 193 Hz.

Step-by-step explanation:

We're dealing with a classic example of the Doppler Effect, which describes the change in frequency of a wave in relation to an observer who is moving relative to the wave source. In this case, the wave source is the train's horn, and the observer is a person at a crossing.

Calculating the Speed of the Train

According to the Doppler Effect formula for a source moving towards a stationary observer, the observed frequency (fobs) is given by:

fobs = fs * (v / (v - vs))

Where:
fs = source frequency (200 Hz)
v = speed of sound in air (335 m/s)
vs = speed of the source (the train)
fobs = observed frequency (208 Hz)

Plugging in the known values and solving for vs, we get:

208 Hz = 200 Hz * (335 m/s / (335 m/s - vs))
vs = (335 m/s * 200 Hz / 208 Hz) - 335 m/s
vs approx 14.9 m/s

The speed of the train is approximately 14.9 m/s.

Calculating the Observed Frequency as the Train Moves Away

After the train passes the crossing, the formula for the observed frequency changes to:

fobs' = fs * (v / (v + vs))

Plugging in the previously found speed of the train, we find the new observed frequency:

fobs' = 200 Hz * (335 m/s / (335 m/s + 14.9 m/s))
fobs' approx 193 Hz

The frequency the observer receives as the train moves away is approximately 193 Hz.

Answer 2

(a) 12.9m/s

(b) 193Hz

Step-by-step explanation:

The principle and concept of this question is based on Doppler's effect.

Doppler's effect is a change in the observed frequency of a wave when the source or the observer move relative to the transmitting medium. Doppler's effect can be expressed mathematically as;

`f = ((U ± U_(0) )/(U ± U_(s) ))f_(0)`

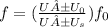
Where,

f is given in terms of the sound frequency f₀

U is the speed of sound in the medium

U₀ is the speed of the observer

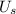`U_(s)` is the speed of the source

When applying Doppler's equation, the signs U₀ and
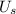`U_(s)` depend on the direction and velocity of of the observer and the source.

+ Positive sign, for U₀ and
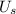`U_(s)` if the velocity one is moving towards the other.

- Negative sign, for U₀ and
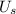`U_(s)` if the velocity one is moving away from the other.

Now, let's applying this information to the question given.

Given:

Frequency of the train's horn, f₀ = 200Hz

Speed of sound , U = 335m/s

Frequency of the approaching train's horn the observer received, f = 208Hz

Since the observer is waiting at the crossing, he/she is at a stationary position.

So, the speed of the observer, U₀ = 0

(a) The train approaches the observer. Following the sign rule, the speed of the source
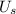`U_(s)` is + positive. Applying this to the equation,

`f = ((U - 0)/(U - (+U_(s)) ))f_(0)`

`f = ((U)/(U - U_(s) ))f_(0)`

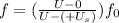
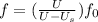
Solving for
`U_(s)`,

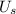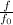`(f)/(f_(0))`= (\frac{U}{U - U_{s}})[/tex]

`{f_(0)U=f(U - U_(s))`

`{f_(0)U=fU - fU_(s)`

`fU_(s) =fU - f_(0)U`

`fU_(s) = U(f - f_(0))`

`U_(s) =(U(f - f_(0)))/(f)`

`U_(s) =(335m/s(208Hz - 200Hz))/(208Hz)`

`U_(s) =(335m/s × 8Hz)/(208Hz)`

`U_(s) =(2680)/(208)`

`U_(s) =12.8846m/s`

`U_(s) =12.9m/s`

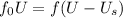
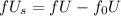
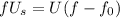
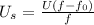
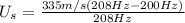
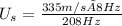
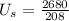
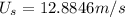
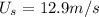
(b) The speed train approaches the observer. Following the sign rule, the speed of the source
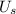`U_(s)` is - negative. Applying this to the equation,

`f = ((U)/(U - (-U_(s)) ))f_(0)`

`f = ((U)/(U + U_(s)))f_(0)`

`f = ((335m/s)/(335m/s + 12.9m/s))200Hz`

`f = ((335m/s)/(335m/s + 12.9m/s))200Hz`

`f = ((335m/s)/(347m/s))200Hz`

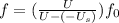
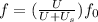
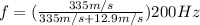
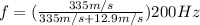
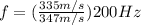
f = 193Hz