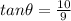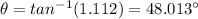Answer:
The angle as calculated is

Solution:
As per the question:
Mass of falcon,

Mass of raven,

Initial speed of the falcon,
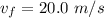
Initial speed of the raven,
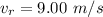
Rebounding speed of the falcon,
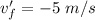
Now,
To calculate the angle at which the direction of motion of the raven changes:
By using the principle of conservation of momentum:
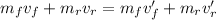
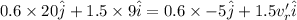
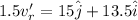
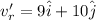
The angle of the change of the raven's direction is given by: