Answer:
The range is [9,-3,-9]
Explanation:
we have the relation
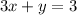
To find the range determine the value of y for each value of x in the relation
so
For x=-2
substitute in the equation
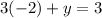
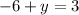
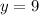
For x=2
substitute in the equation
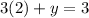
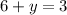
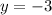
For x=4
substitute in the equation
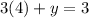
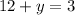
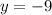
therefore
The range is [9,-3,-9]