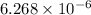Answer:
0.00903 rad
0.00926 rad
6.268\times 10^{-6}
Step-by-step explanation:
s = Diameter of the object
r = Distance between the Earth and the object
Angle subtended is given by
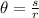
For the Moon
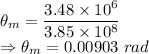
The angle subtended by the Moon is 0.00903 rad
For the Sun
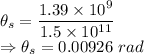
The angle subtended by the Sun is 0.00926 rad
Area ratio is given by
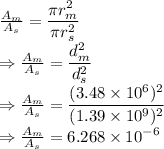
The area ratio is