Question

Some cookware has a stainless steel interior (α=17.3×10−6K−1) and a copper bottom (α=17.0×10−6K−1) for better heat distribution. Suppose an 8.0-in. pot of this construction is heated to 620 ∘C on the stove. Part A If the initial temperature of the pot is 22 ∘C, what is the difference in diameter change for the copper and the steel?

Answer 1

0.0014352 inch

Step-by-step explanation:

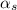`\alpha_s` = Coefficient of linear expansion of steel =
`17.3* 10^(-6)\ /K`

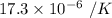
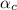`\alpha_c` = Coefficient of linear expansion of copper =
`17* 10^(-6)\ /K`

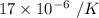
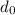`d_0` = Original diameter = 8 in

`\Delta T` = Change in temperature

Change in diameter of steel

`\Delta d_s=\alpha_sd_0\Delta T\\\Rightarrow \Delta d_s=17.3* 10^(-6)* 8* (620-22)\\\Rightarrow \Delta d_s=0.0827632\ in`

Change in diameter of copper

`\Delta d_c=\alpha_sd_0\Delta T\\\Rightarrow \Delta d_c=17* 10^(-6)* 8* (620-22)\\\Rightarrow \Delta d_c=0.081328\ in`

Difference in diameter is given by

`\Delta d=\Delta d_s-\Delta d_c\\\Rightarrow \Delta d=0.0827632-0.081328\\\Rightarrow d=0.0014352\ in`

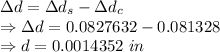
The difference in diameter change for the copper and the steel is 0.0014352 inch