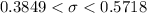Question

The percentage of titanium in an alloy used in aerospace castings is measured in 51 randomly selected parts. The sample standard deviation is s = 0.46. Construct a 95% two-sided confidence interval for σ. Assume population is approximately normally distributed.

Answer 1

Answer:
`0.3849<\sigma<0.5718`

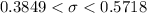
Explanation:

Given : sample size : n= 51

sample standard deviation : s= 0.46

Significance level :
`\alpha=1-0.95=0.05`

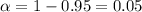
Using chi-square distribution, the critical values will be :

`\chi^2_(\alpha/2, n-1)=\chi_(0.025,\ 50)=71.4202`

`\chi^2_(1-\alpha/2, n-1)=\chi_(0.975,\ 50)=32.3574`

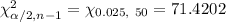
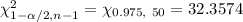
Confidence interval for population standard deviation (
`\sigma`) :

`\sqrt{(s^2(n-1))/(\chi^2_(\alpha/2))}<\sigma<\sqrt{(s^2(n-1))/(\chi^2_(1-\alpha/2))}`

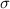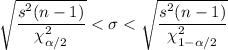
Substitute all the values , we get

`\sqrt{((0.46)^2(50))/(71.4202)}<\sigma<\sqrt{((0.46)^2(50))/(32.3574)}\\\\ √(0.148137361699)<\sigma<√(0.326973118977)\\\\\approx0.3849<\sigma<0.5718`

Hence, the 95% two-sided confidence interval for σ :
`0.3849<\sigma<0.5718`