Answer: 97
Explanation:
The formula to find the sample size:-
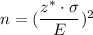 , where
, where
 = prior standard deviation., z^*= Critical value corresponds to the confidence level and E is margin of error .
= prior standard deviation., z^*= Critical value corresponds to the confidence level and E is margin of error .
Given : A psychologist estimates the standard deviation of a driver's reaction time to be 0.05 seconds.
i.e.

E= 0.01
Critical value for 95% confidence interval = 1.96
Then, the required sample size will be
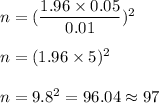 [Round to the nest integer.]
[Round to the nest integer.]
Hence, the required minimum sample size = 97