Answer:
The slope of the line is 0.
Explanation:
Let the coordinates of point P be (
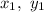 ) and point Q be (
) and point Q be (
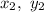 ), then the slope of the line passing through both points P and Q is
), then the slope of the line passing through both points P and Q is
 .
.
Therefore, the slope of the line that passes through the points (3, 1) and (0, 1) is
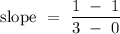
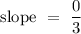
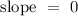 .
.
Notice that both points, in this case, have the same y-coordinate which is 1. This indicates that the line is a horizontal line parallel to the x-axis which has a slope of 0.
If the two points in which a line passes through share the same x-coordinate, the resulting line is a vertical line parallel to the y-axis which has an undefined slope since
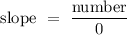 ,
,
where the x-coordinate of both points cancels out to give a zero in the denominator. (Remember you cannot divide a number by zero!)