Answer:
f(x) =

Explanation:
The given options are,
a) f(x) =
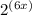
b) f(x) =

c) f(x) =
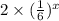
d) f(x) =
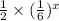
Now, clearly a) is a monotonically increasing function, hence discarded, and both of c) and d) don't pass through (0, 1) hence they are also discarded.
Only b) is a decay function which does also pass through (0, 1), hence, b) is the correct option.