Answer: 68
Explanation:
Formula for sample size when prior estimate of population proportion (p) is available:

, where z*= critical-value.
E= Margin of error.
Let p be the population proportion of trees are infected with the citrus red mite.
As per given , we have
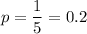
E= ± 0.08
The critical z-value corresponding to 90% confidence level = z*=1.645
Substitute all the values in the above formula , we get
Required sample size :
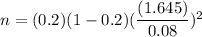
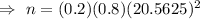
 [Rounded to next integer.]
[Rounded to next integer.]
Thus, the minimum sample size should be taken =68