Question

Caden and collin had 60 gifts altogether. If caden gave collin 12 of his gifts and collin gave 10 of his gifts to caden, caden would have 3 times as many as collin. How many gifts did each if the boys start with?

Answer 1

Caden had 47 gifts and Collin had 13 gifts at the start.

Explanation:

Given:

Caden and Collin had 60 gifts altogether.

Let number of gifts of Caden had be x

also Let number of gift Collin had be y.

Hence the equation can be framed as;

`x+y=60 \ \ \ \ equation \ 1`

Also given Caden gave Collin 12 of his gifts and Collin gave 10 of his gifts to Caden, Caden would have 3 times as many as Collin.

Hence the equation can be framed as;

`((x-12)+10)=3((y-10)+12)`

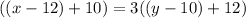
Now Solving the above equation we get;

`x-12+10=3(y-10+12)\\x-2=3(y+2)\\x-2=3y+6\\x-3y=6+2\\x-3y=8 \ \ \ \ equation \ 2`

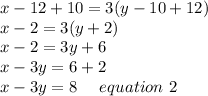
Now Subtracting equation 2 from equation 1 we get;

`(x+y)-(x-3y)=60-8\\x+y-x+3y=52\\4y=52\\y = (52)/(4)=13`

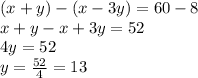
Now Substituting the value of y in equation 1 we get;

`x+y=60\\x+13=60\\x=60-13\\x=47`

Hence Caden had 47 gifts and Collin had 13 gifts at the start.