Question

Does anyone know the answer??

Answer 1

x = -1 or x = 7

is the required solution of 4|x - 3| - 8 = 8

Explanation:

Given:

4|x - 3| - 8 = 8

To Find:

x = ?

Solution:

We have

4|x - 3| - 8 = 8

∴
`\therefore 4|x - 3| - 8 = 8\\\therefore 4|x - 3| = 8 + 8\\\therefore |x - 3| =(16)/(4)\\ \therefore |x - 3| =4`

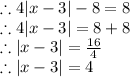
As there is Modulus sign MOD has two values i.e one with positive value and other with negative value.

∴
`(x-3) =4\ or\ (x-3)=-4\\\therefore x =4+3\ or\ x=3-4 \\\therefore x =7\ or\ x =-1`

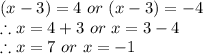
x = -1 or x = 7

is the required solution of 4|x - 3| - 8 = 8