Question

The owner of a company that manufactures drinking cups decides it would be impressive to build an inground swimming pool that is a scaled up version of her best selling cup. For this particular cup, the area of the circular opening at the top is 1.50 times the area of the circular bottom. Her pool contractor informs her that when the pool is full of water, the magnitude of the force acting on the top surface will be the same as the magnitude of the force acting on the bottom surface. Determine the depth of the pool.

Answer 1

The depth is 5.15 m.

Step-by-step explanation:

Lets take the depth of the pool = h m

The atmospheric pressure ,P = 101235 N/m²

The area of the top = A m²

The area of the bottom = a m²

Given that A= 1.5 a

The force on the top of the pool = P A

The total pressure on the bottom = P + ρ g h

ρ =Density of the water = 1000 kg/m³

The total pressure at the bottom of the pool = (P + ρ g h) a

The bottom and the top force is same

(P + ρ g h) a = P A

P a +ρ g h a = P A

ρ g h a = P A - P a

`h=(P ( A-a))/(\rho g a)`

`h=(P ( 1.5 a-a))/(\rho g a)`

`h=(P ( 1.5- 1))/(\rho g)`

`h=(101235 ( 1.5- 1))/(1000* 9.81)\ m`

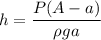
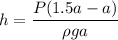
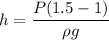
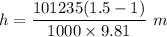
h=5.15 m

The depth is 5.15 m.