Answer:
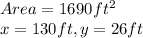
Explanation:
Given the costs we can form an equation:

and fencing is triangular such that the area enclosed can be written as:
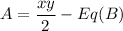
- First need to convert the above equation so that it is only in terms of one variable. [either x or y]
To make the equation only in terms of
 we can substitute
we can substitute
 from Eq(A) i.e,
from Eq(A) i.e,
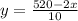 , to Eq(B)
, to Eq(B)
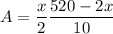
simplify

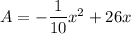
- Now, in order to find the maximum area enclosed we can find
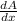 and equate it zero.
and equate it zero.
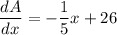
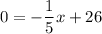
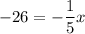
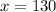
we have the length of one dimension: specifically, the lower fence will be

we can use this value of
 to find the corresponding value of
to find the corresponding value of
 . From Eq(A)
. From Eq(A)

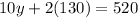


the length of the left fence will be
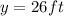
- The enclosed area by the fence will be

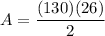

Hence the maximum area that can enclosed by the fences provided the costs will be
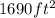
- You can even check the cost of the dimensions whether they all add up to $520 or not.
Use Eq(A)

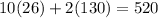
and indeed it does!