Question

Consider the construction of a pen to enclose an area. You have 600 ft of fencing to make a pen for hogs. If you have a river on one side of your property, what are the dimensions (in ft) of the rectangular pen that maximize the area? shorter side ft longer side ft

Answer 1

150 ft x 300 ft

Explanation:

Let x be the length of each of the two sides perpendicular to the river and y be the length of the size parallel to the river.

The total length of fencing is given by:

`2x+y=600\\y= 600-2x`

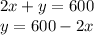
The area of rectangular pen is:

`A = xy\\A=x(600-2x)\\A= 600x -2x^2`

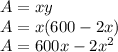
Finding the value of x for which the derivative of the area function is zero gives us the value of x needed to maximize the area:

`(dA(x))/(dx) =(d(600x -2x^2))/(dx)\\0= 600 - 4x\\x= 150`

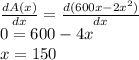
For x=150, the value of y is:

`y= 600-2x=600-(2*150)\\y=300`

The dimensions that maximize the area are 150 ft x 300 ft.