Two fair dice, one blue and one red, are tossed, and the up face on each die is recorded. Define the following events: E:{ The numbers are equal } F:{ The sum of the numbers is …

Question

asked Aug 25, 2020 185k views

1 Answer

IDDQD · Answer 1 · 2020-08-30T23:46:03+0000

Answer:

(i) 1/6

(ii) 1/2

(iii) 1/6

Step-by-step explanation:

When two fair dice are tossed,

Total possible outcomes,

n(S) = 6 × 6 = 36, ( ∵ outcome when a dice is tossed = 6 )

(i) If E = {The numbers are equal }

= { (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}

⇒ n(E) = 6,

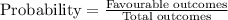
$\text{Probability}=\frac{\text{Favourable outcomes}}{\text{Total outcomes}}$

Thus,

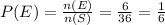
P(E) =(n(E))/(n(S))=(6)/(36)=(1)/(6)

(ii) Since, even + even = even and odd + odd = even,

If F = {The sum of the numbers is even}

F = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (1, 3), (1, 5), (2, 4), (2, 6), (3, 1), (3, 5), (4, 2), (4, 6), (5, 1), (5, 3), (6, 2), (6, 4)}

⇒ n(F) = 18,

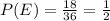
P(E) =(18)/(36)=(1)/(2)

(iii) E∩F = E,

⇒ n(E∩F) = 6,

$P(E\cap F) =(1)/(6)$