Answer:
a) M = 2 10³⁰ kg , b)
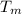 = 5.81 10⁷ s
= 5.81 10⁷ s
Step-by-step explanation:
a) For this exercise let's use Newton's second law where force is the law of universal gravitation and acceleration is centripetal
G m M / R² = m a
a = v² / R
G M / R = V²
The orbit of the two planets is approximately circular, therefore the velocity module (speed) is constant
v = d / t
The distance is the length of the circular orbit
d = 2π R
G M / R = 4π² R² / T²
G M T² = 4π² R³
Let's write this equation for each planet
For the earth
The period is T = 3.16 10⁷ s and the radius of the orbit R = 1.5 10¹¹ m, let's calculate the mass of the sun
M = 4π² R³ / G T²
M = 4π² (1.5 10¹¹)³ / (6.67 10⁻¹¹ (3.16 10⁷)²)
M = 133.24 10³³ / 66.60 10³
M = 2 10³⁰ kg
b) For this part we write this equation for the two points
For the earth
 ² = (4π² / G M)
² = (4π² / G M)
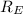 ³
³
For mars
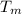 ² = (4π² / G M)
² = (4π² / G M)
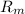 ³
³
Let's divide the two expressions
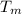 ² /
² /
 ² =
² =
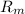 ³ /
³ /
 ³
³
They indicate that the orbit of Mars is
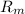 = 1.5
= 1.5
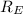
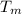 ² /
² /
 ² = (1.5
² = (1.5
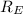 /
/
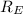 )³
)³
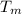 ² =
² =
 ² 1.5³
² 1.5³
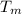 ² = (3.16 10⁷)² 1.5³
² = (3.16 10⁷)² 1.5³
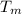 = √ (33.70 10¹⁴)
= √ (33.70 10¹⁴)
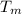 = 5.81 10⁷ s
= 5.81 10⁷ s