Question

An airplane is flying in a horizontal circle at a

speed of 100 m/s. The 80.0 kg pilot does not
want the centripetal acceleration to exceed
6.92 times free-fall acceleration.
Find the minimum radius of the plane’s
path. The acceleration due to gravity is 9.81
m/s2
.

Answer 1

the minimum radius of the plane path would be 147.45 meters.

Step-by-step explanation:

given speed of the plane = 100 m/s.

and centripetal acceleration ≤ 6.92×g

we know that centripetal acceleration =
`(v^(2))/(r)`

therefore
`(v^(2))/(r)\leq 6.92* 9.81\\`

therefore
`r\geq (100* 100)/(6.92* 9.81)`

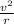
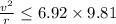
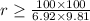
therefore r ≥ 147.54 meters